L’expérience de Foucault repose sur ce principe : un observateur qui se trouve devant un pendule en oscillation tourne avec la Terre, ainsi qu’avec son environnement, les murs, le plafond et le sol sans s’en apercevoir. En revanche, le pendule, lui, oscille toujours dans la même direction. Ainsi, il devient un repère, un invariant, qui nous permet de percevoir ce mouvement de rotation. Nous avons la sensation de voir le pendule tourner, mais c’est en fait notre planète qui le fait. Ton petit pois a bien intégré ? Aller, une petite explication supplémentaire :

Allez, la même chose en dessins, ho là là, qu’est-ce que je ne ferai pas pour toi !

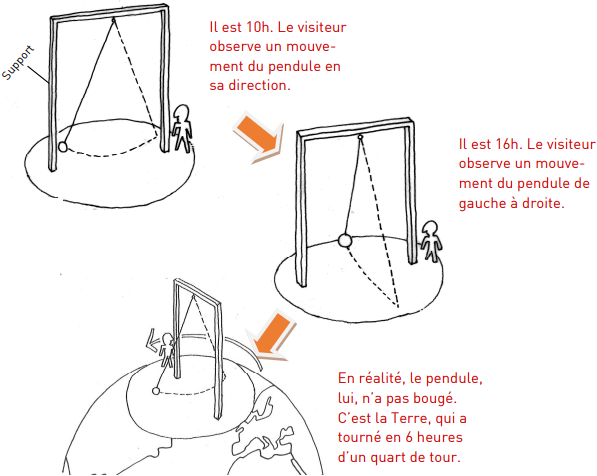
Puisque le plan d’oscillation du pendule est indépendant de la rotation de la Terre, son plan d’oscillation est aussi fixe que le sont les étoiles dans le ciel. En effet, les étoiles ne bougent pas c’est la Terre qui tourne et donne l’impression d’un déplacement des étoiles.

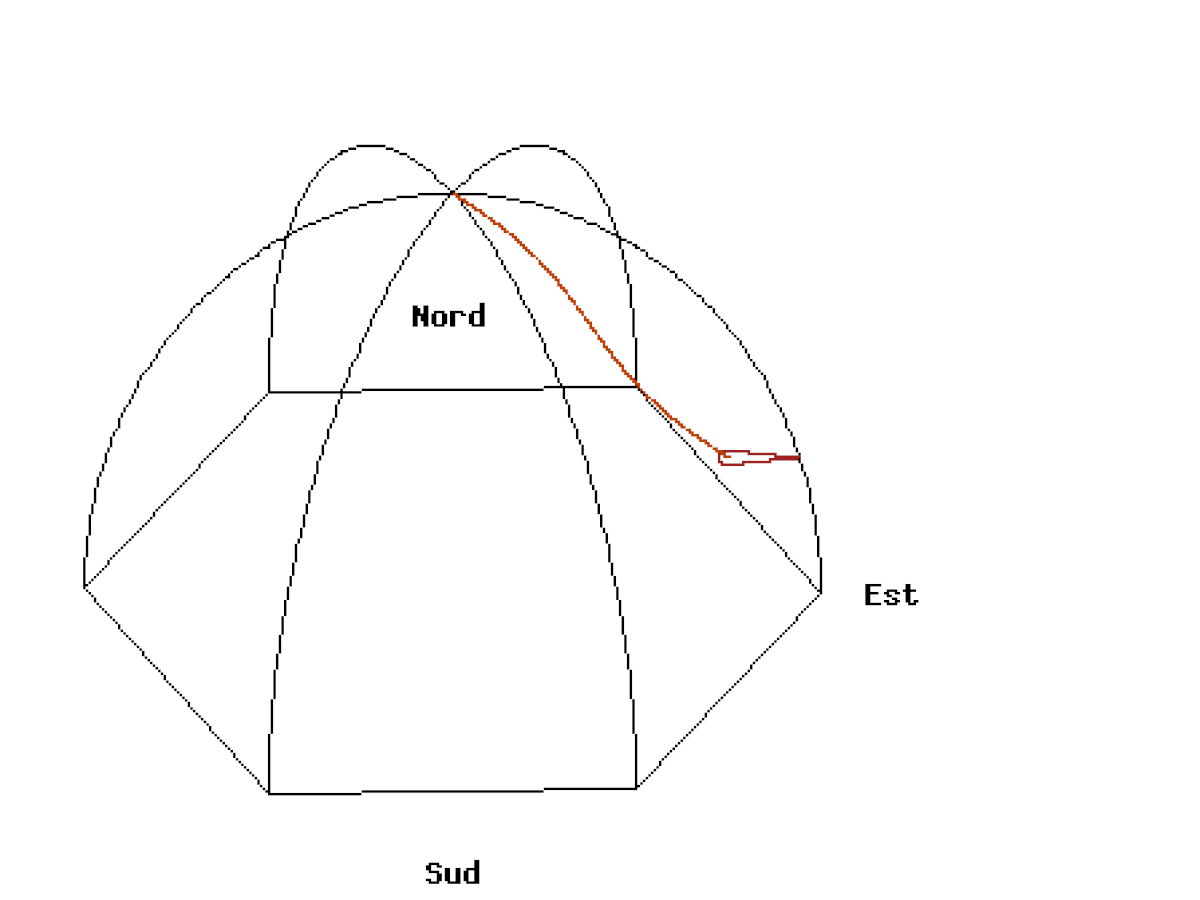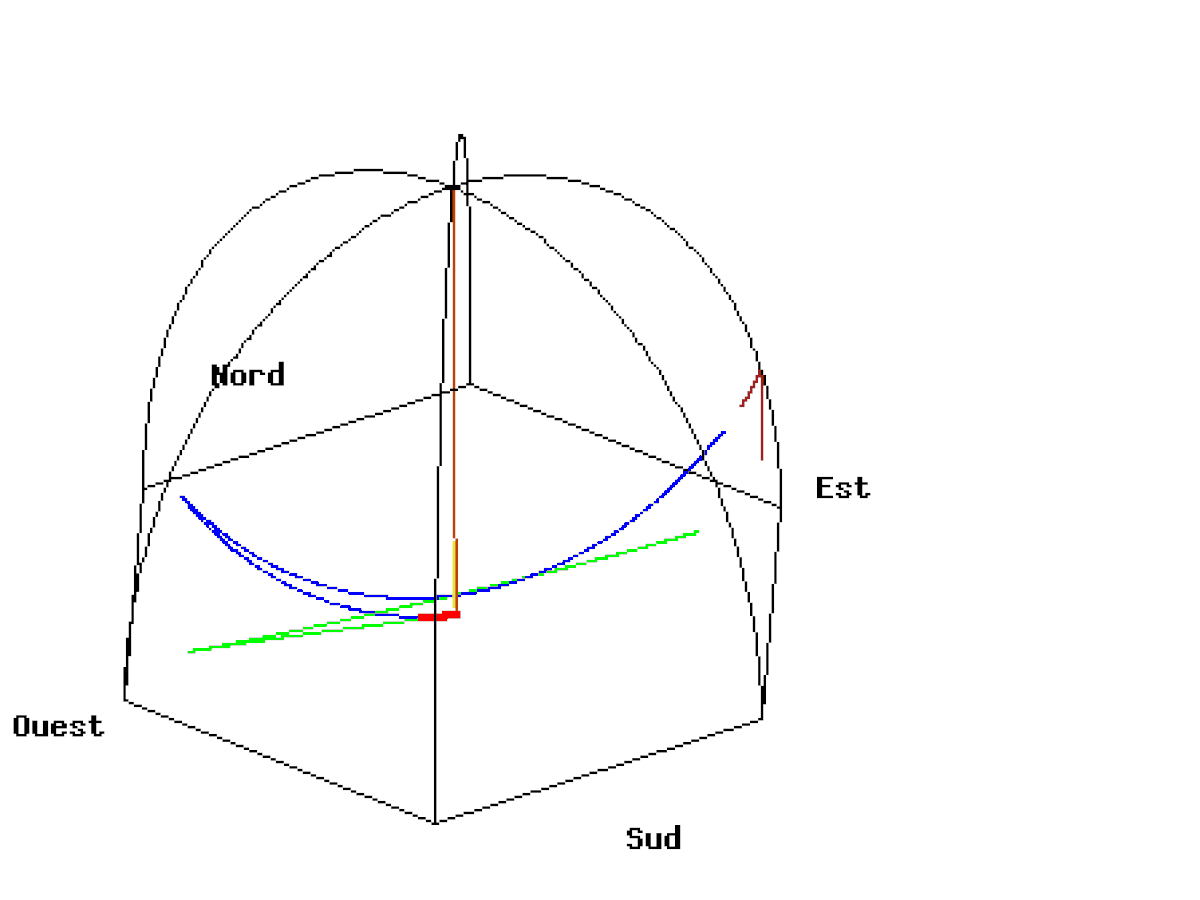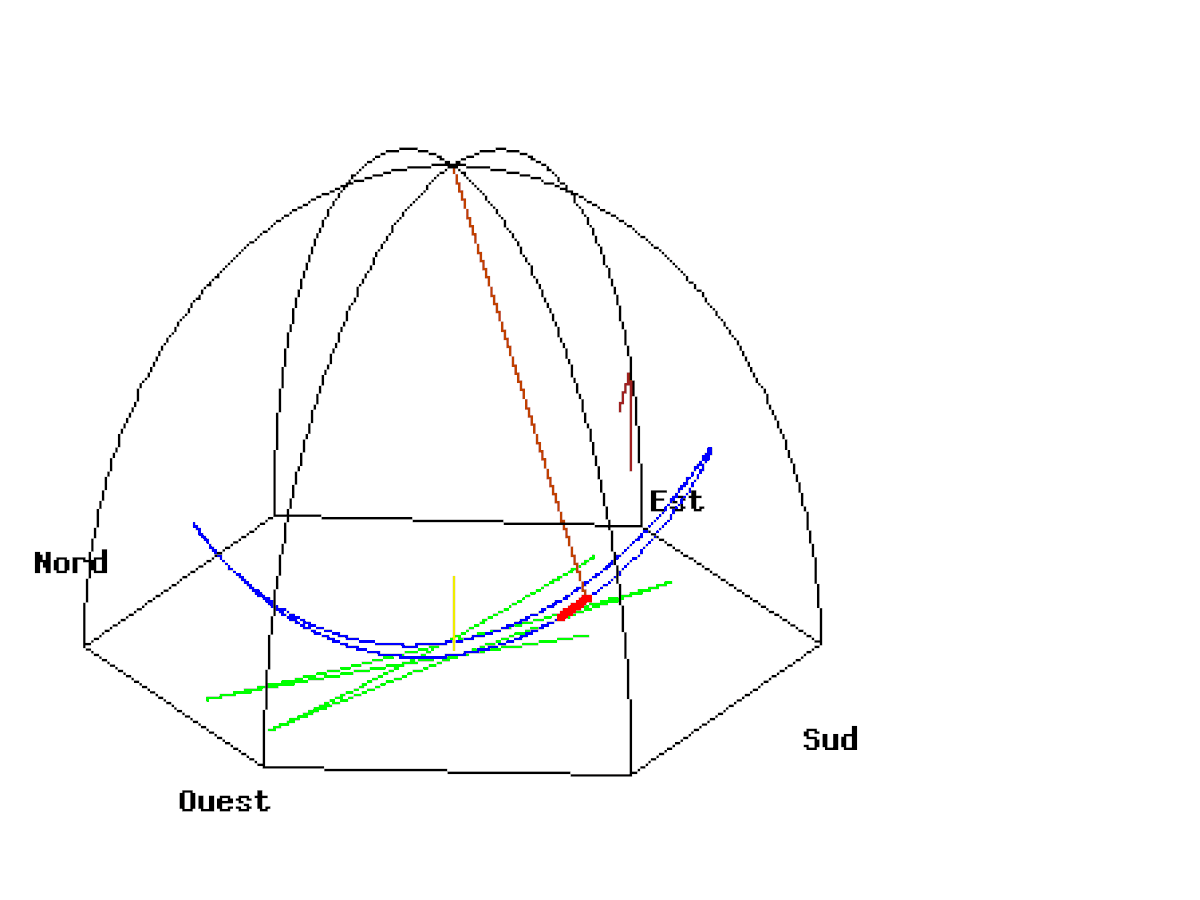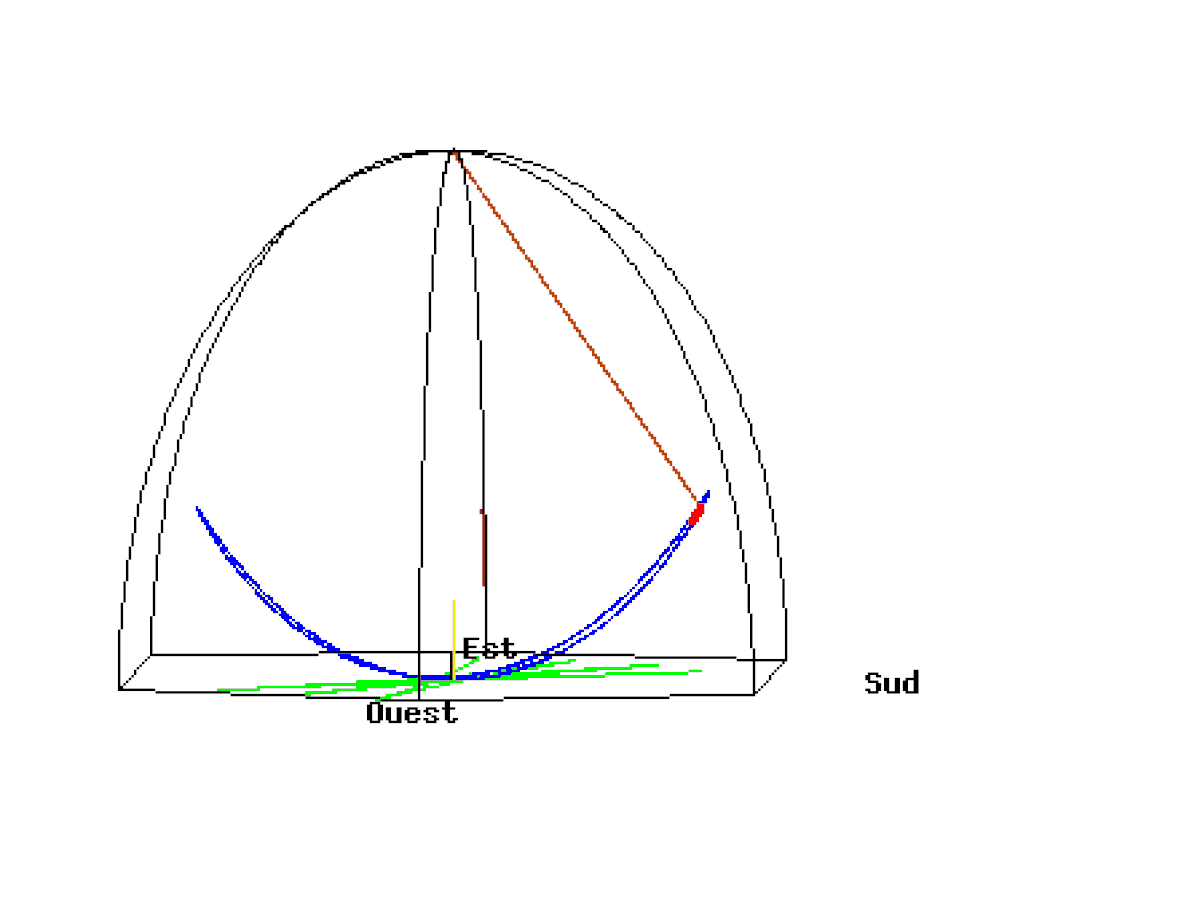
La petite vidéo ci-dessous prend une petite tranche de ciel, et situe le pendule par rapport à cette tranche et le plan du pendule ne varie pas par rapport aux étoiles. Absolument extraordinaire !

La tranche de ciel considéré dans la démonstration ci-dessous représente la Petite Ourse (Kis Medve), la Grande Ourse (Nagy Medve), Cassiopée (Cassiopea), l’étoile Polaire (Polaris) qui est une supergéante huit fois plus massive que notre Soleil et 2 000 fois plus lumineuse.

Le texte en italique rouge dans la fenêtre déroulante ci-dessous donne quelques précisions supplémentaires techniques. Tu peux ne pas les lire, cela n’influencera pas la suite de la lecture du pendule de Foucault. Dans ce cas, reprends après la fenêtre déroulante, la lecture en lettres noires et droites.

  

MAINTENANT IL FAUT PRÉCISER CERTAINES DONNÉES.

Durée d’oscillation du pendule

Ce pendule, d’une grande inertie, pouvait osciller longtemps avant de s’arrêter. Mais pour que l’expérience dure longtemps il faut entretenir cette oscillation. Il y a deux méthodes : la bobine toroïdale en haut du câble et l’électroaimant en bas au centre d’oscillations, le tout avec une détection du passage du pendule et une activation de l’électroaimant au bon moment pendant la bonne durée.

Aujourd’hui on trouve généralement un mécanisme magnétique (électroaimant), placé au-dessous du pendule, sous la table, et qui permet d’entretenir le mouvement car en raison des frottements de l’air celui du Panthéon n’oscille que durant 6 heures. Je rassure déjà les futures remarques, l’électroaimant n’a aucune influence sur l’orientation, les oscillations, et sur les éventuelles directions que pourrait prendre le pendule. Il est totalement neutre. Ceci est largement démontré.

D’ailleurs, pour l’Exposition universelle de Paris, en 1855, Foucault installe, cette fois lui-même, dans le Palais de l’Industrie un pendule assisté électromagnétiquement. C’est ce pendule, remonté dans la chapelle de l’ancienne abbaye de Saint-Martin-des-Champs, qui continue à faire les délices des visiteurs du Musée des arts et métiers.

Le pendule de Foucault était exposé au Musée National d’Histoire Américaine du Smithsonian aux Etats-Unis, pendant de nombreuses années (il a été retiré fin 1998).

Le texte en italique rouge dans la fenêtre déroulante ci-dessous donne quelques précisions supplémentaires techniques. Tu peux ne pas les lire, cela n’influencera pas la suite de la lecture du pendule de Foucault. Dans ce cas, reprends après la fenêtre déroulante, la lecture en lettres noires et droites.

Durée "d’une journée de pendule"

On pourrait s’attendre à ce que 24 heures soit nécessaires pour réaliser un tour complet autour du plan d’oscillation, comme une horloge. Ben, pas du tout mon pote ! Enfin à Paris. Dans cette (ancienne) belle ville, il faut, en apparence je dis bien en apparence, 32,7 heures pour que la table des repères horaires fasse le tour et l’expérience a été faite des centaines de fois à Paris et a montré toujours le même résultat. À Casablanca pour que le pendule fasse le tour de l’horloge il faut 43 heures, au Caire 48 heures, et plus on s’approche de l’Équateur plus le temps augmente.

A l’Équateur, le pendule est perpendiculaire à l’axe de rotation de notre planète et, en apparence, il ne dévie plus. Ainsi le sol qui se trouve au-dessous du pendule tend vers l’infini.

Et puis, lorsque notre pendule prend la direction du pôle sud en partant de l’Équateur, il se remet à dévier, en apparence. La durée nécessaire pour faire le tour complet du cadran se remet à diminuer pour revenir à 24 heures au pôle Sud géographique. À cet endroit, pour l’observateur à côté du pendule, le pendule se déplacera dans le sens inverse des aiguilles d’une montre.

On est en plein dans le contre intuitif. Mais alors, que se passe t-il, serait-ce la fin des temps établis ?

Lorsque Foucault lui-même s’est rendu compte que la table des repères horaires fasse le tour en 32,7 heures lors de son expérience, il n’en a pas dormi de la nuit, le pauvre ! Mais, comme je tiens à ce que tu dormes bien, soit tranquille, ami passionné. C’est une question de latitude, tout simplement.

Importance de la latitude

Rafraichissons nos souvenirs de primaire, je te demande ci-dessous si tu le savais, mais bien sûr que oui !!

 

Que se passe-t-il aux pôles ?

Au pôle Nord (latitude : 90° Nord) la verticale du point de suspension du pendule coïncide avec l’axe de rotation de la Terre, autrement dit, le plan d’oscillation du pendule est en rotation autour de l’axe de la verticale du lieu. Un observateur tourne avec la Terre et reste fixe par rapport au sol. Pour lui c’est l’axe d’oscillation du pendule qui tourne.

Ce même observateur qui se trouve ainsi au pôle Nord fait le tour complet en 24 heures (plus exactement en un jour sidéral, soit 23 heures 56 min), dans le sens horaire (c’est-à-dire dans le sens inverse de la rotation de la Terre), par rapport au plan d’oscillation du pendule (dont on reprécise que ce plan d’oscillation ne change jamais de direction quel que soit la direction dans laquelle il est lancé).

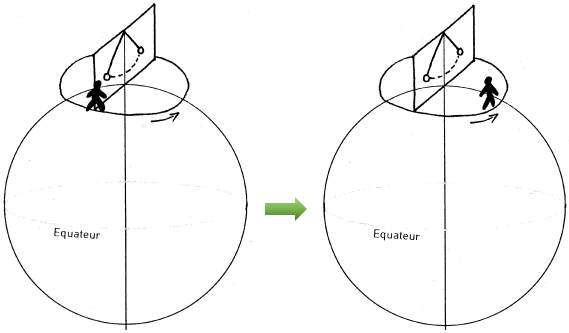
Le pendule oscille dans un plan fixe par rapport aux étoiles alors que dessous, la Terre tourne indépendamment. Sa vitesse de rotation est d’environ 15° par heure.

Pour ceux que cela intéresse le vecteur Ω est la composante verticale de la rotation de la Terre, décomposé en ΩV (verticale) et ΩH (horizontale).

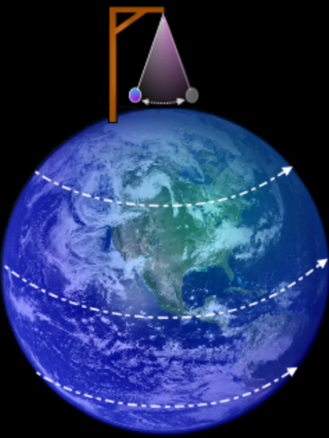
Au pôle Sud (latitude : 90° Sud), il se passe la même chose mais dans le sens inverse, it is not complicado !

Latitudes intermédiaires

Plus la latitude se rapproche de l’équateur terrestre et plus les pendules mettent du temps pour revenir sur leur axe initial. Commençons par une position hors pôle et hors équateur, soit à une latitude quelconque.

À une latitude donnée le pendule n’oscille pas dans l’axe de rotation de la Terre. Il y a obligatoirement un angle qui est défini par la latitude.

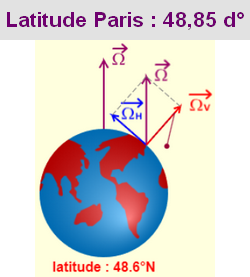
A Paris, le plan du pendule ne revient pas à son point de départ en 24 heures comme on pourrait le croire. A chaque oscillation de 16,42 secondes il se déplace de 5,4 mm dans le sens des aiguilles d’une montre (dans le sens inverse de la rotation de la Terre) et retrouve son point de départ en 31h 48′. Ce n’est pas le plan du pendule qui tourne mais la Terre.

Pour ceux que cela intéresse le vecteur Ω est la composante verticale de la rotation de la Terre, décomposé en ΩV (verticale) et ΩH (horizontale).

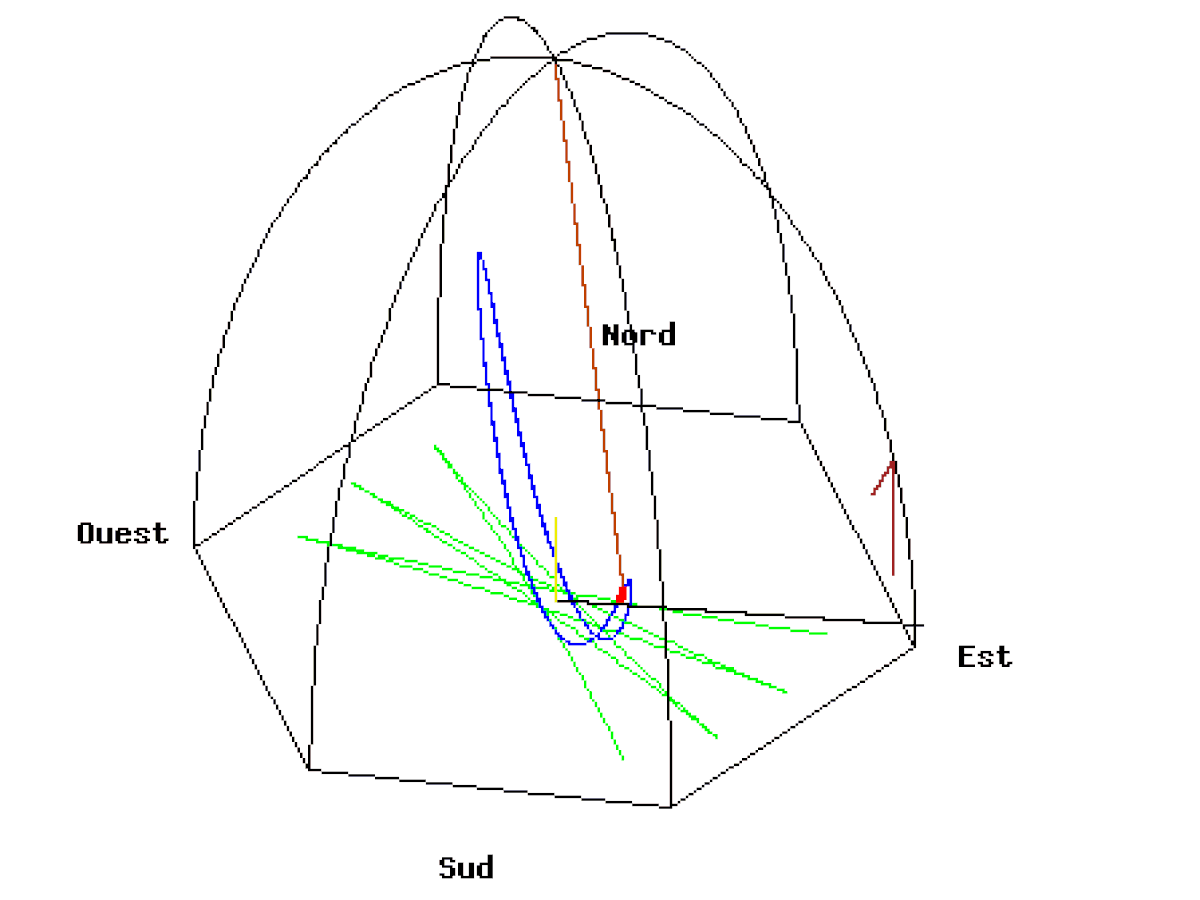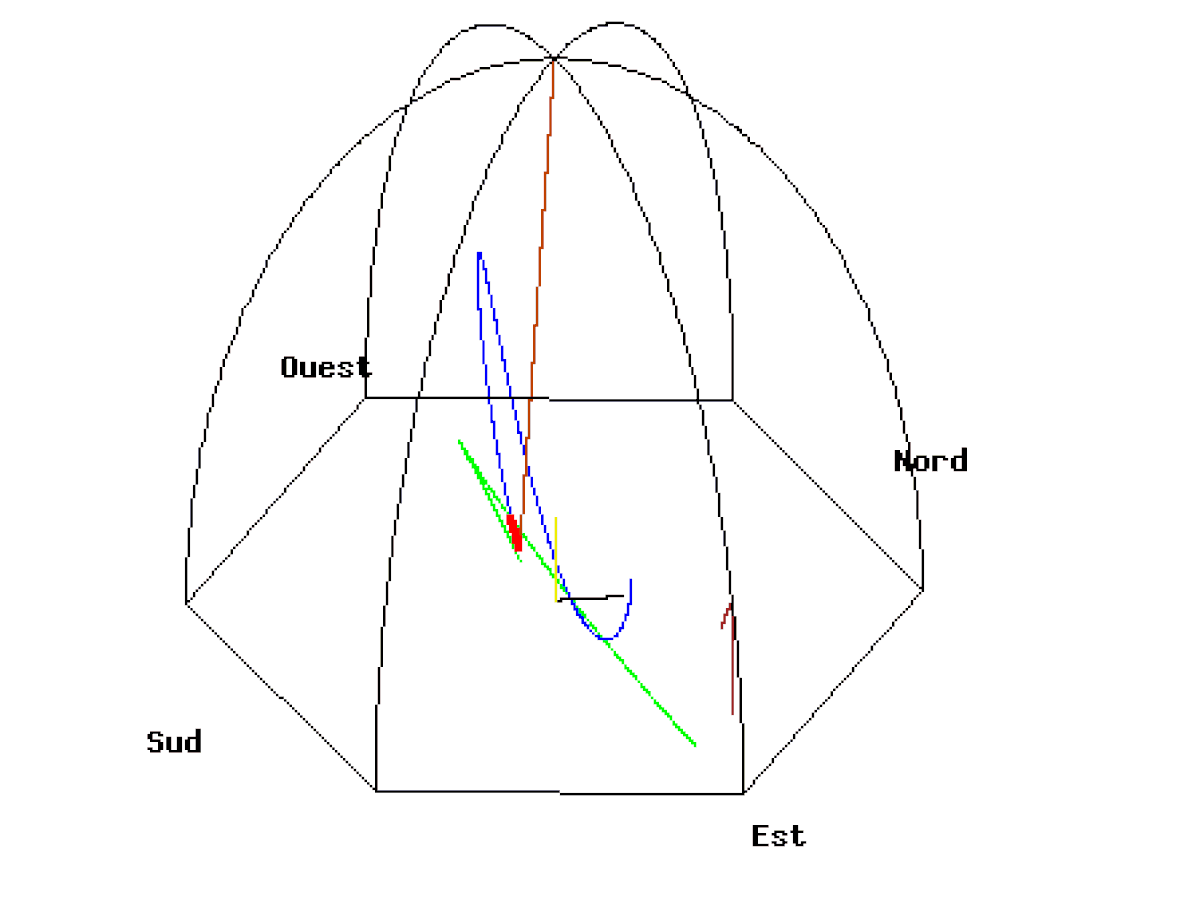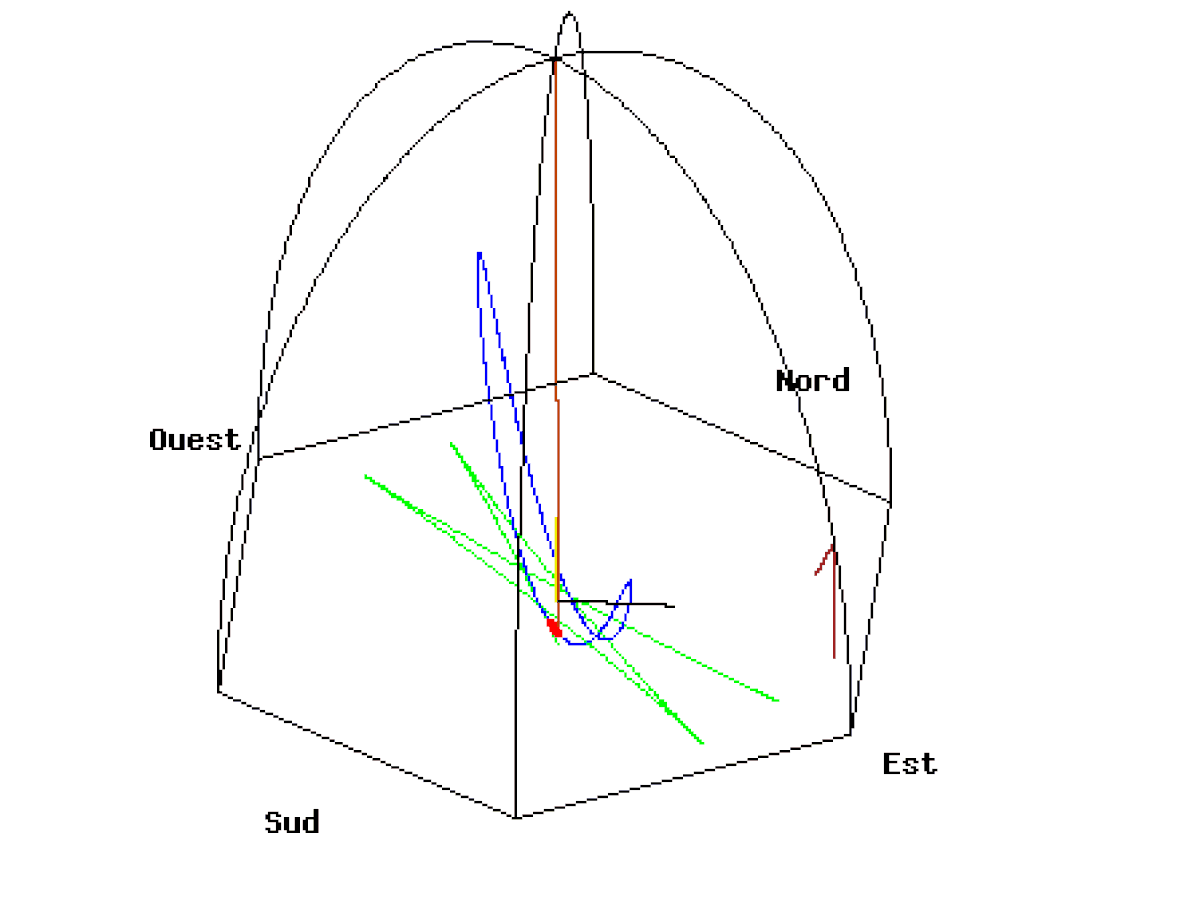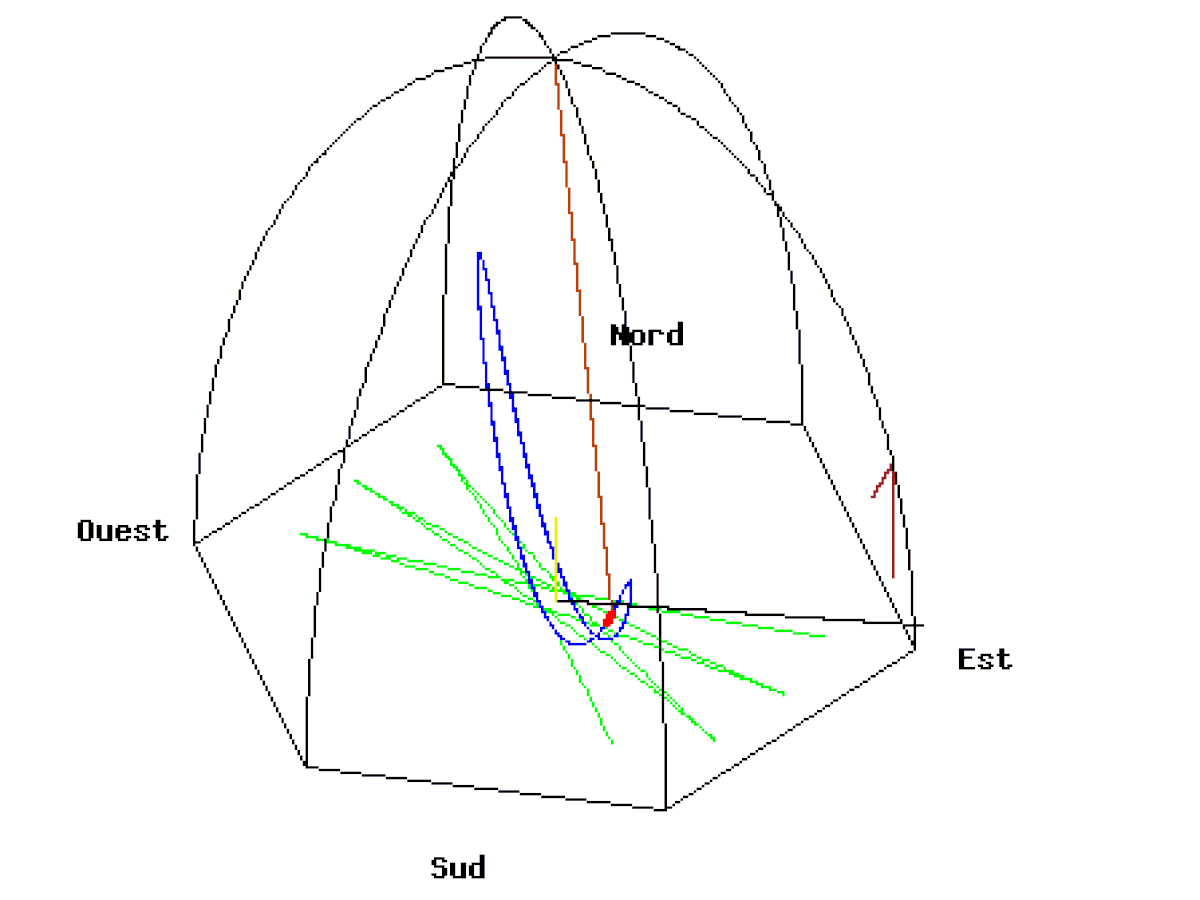
Ci-dessous, deux animations du Pendule de Foucault de 67 mètres lâché au Panthéon de Paris à une distance de 50 mètres à l’est du point d’équilibre avec une vitesse initiale nulle. La vitesse de rotation de la Terre est exagérée (1 tour en 110 secondes). Vue d’une caméra liée au plan d’oscillation.

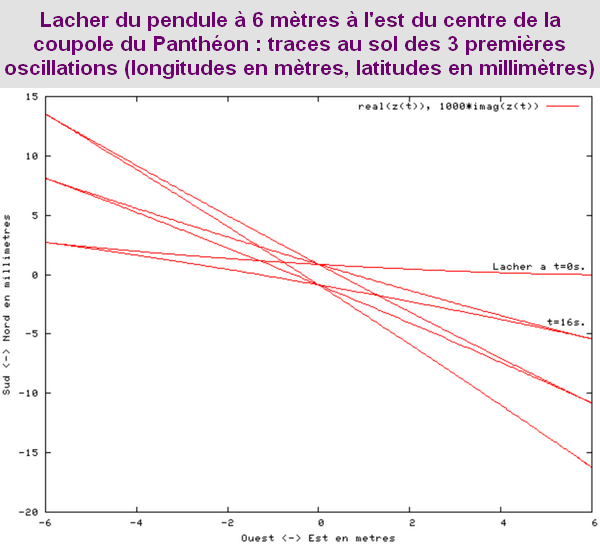
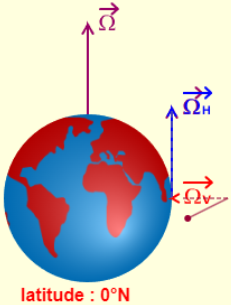
A l’équateur le pendule finit par osciller dans un plan apparemment figé qui ne permet pas de voir la rotation de la Terre. Cette fois-ci, la verticale du pendule est perpendiculaire à l’axe de rotation de la Terre. Le pendule conserve la même direction, puisqu’il reste toujours perpendiculaire à l’axe de rotation. Ainsi, contrairement à ce qui se passe aux pôles, le sol ne tourne pas autour de l’axe du pendule mais transporte l’axe avec lui. Pour un observateur tout se passe comme si le pendule était transporté dans un train et se balançait dans le sens de la marche du train. Le plan du pendule est figé et la Terre ne tourne plus autour. Sa période de révolution tend vers l’infini.

Pour ceux que cela intéresse le vecteur Ω est la composante verticale de la rotation de la Terre, décomposé en ΩV (verticale) et ΩH (horizontale).

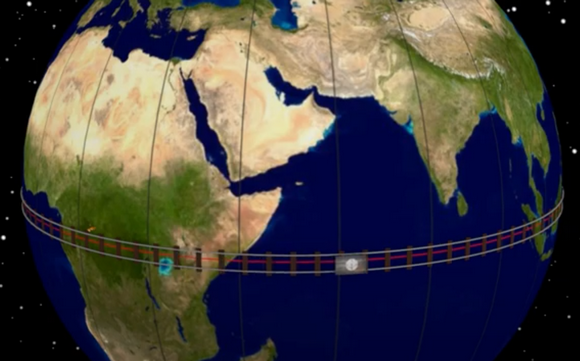
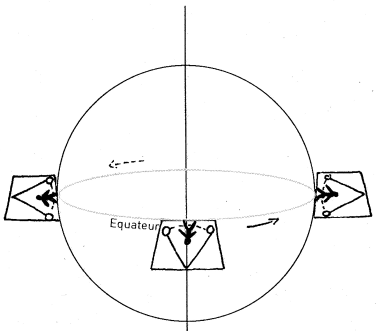
SUITE 2 sur 2

Le pendule de Foucault pose la question de la nature du repère qui sert de référence. En effet, tout mouvement est relatif. Si la Terre est en rotation, elle l’est par rapport à quelque chose. On ne peut pas parler d’un mouvement sans définir un cadre de référence. Ce cadre est un référentiel galiléen, mais comment ce référentiel est-il défini ? Plaçons le pendule Foucault au pôle. La Terre tourne par rapport à un repère galiléen selon l’axe terrestre avec la pulsation Ω. Le pendule tourne par rapport à la Terre avec une pulsation qui vaut au pôle − Ω, selon la verticale du lieu qui est également l’axe terrestre. Le pendule oscille donc dans un plan fixe par rapport à un repère galiléen.

Dans une première approximation, le plan du pendule est fixe par rapport au Soleil. Mais, si Foucault avait réussi à construire un pendule capable d’osciller suffisamment longtemps, disons pendant un mois, il se serait aperçu que le plan d’oscillation dérivait également par rapport à la position du Soleil. Notre étoile ne fait donc pas partie du système de référence en question.

Peut-être faut-il alors considérer les étoiles proches du Soleil ? Mais là aussi, si l’expérience pouvait durer suffisamment longtemps, elle montrerait que le plan des oscillations se déplace nettement par rapport aux étoiles après quelques années. Quel objet choisir dans ce cas ? Le centre galactique, la galaxie d’Andromède, le Groupe Local, le superamas local ? Chacun de ces objets donnerait l’illusion d’être fixe par rapport au plan des oscillations, mais finirait, après un temps de plus en plus long, par révéler une dérive.

Si l’expérience pouvait être menée suffisamment longtemps en considérant comme référence les objets les plus lointains de l’univers, les galaxies ou quasars situés à des milliards d’années-lumière, on pourrait constater encore une infime dérive du plan d’oscillation.

Finalement, l’ultime recours serait de considérer comme référence le rayonnement de fond de l’univers. Avec ce système de référence, et si l’expérience de Foucault était réalisable, le plan des oscillations serait enfin fixe et il n’y aurait plus de dérive. Ce n’est donc qu’en fonction de l’Univers dans son ensemble, que nous pouvons définir un référentiel galiléen par rapport auquel le plan des oscillations est fixe.

Le pendule de Foucault se moque donc de la présence du Soleil ou de la Galaxie. Son mouvement lui est directement dicté par l’Univers entier. Cette expérience met en évidence une sorte de lien mystérieux entre chaque point et l’Univers tout entier et Ernst Mach s’est posé la question de savoir quelle serait la Mécanique dans un Univers vide (voir Principe de Mach). Jusqu’à nouvel ordre, la nature de ce lien reste inconnue.

En effet, tout pendule est constitué d’un câble ou d’un fil ou d’une corde et d’une masselotte. Pour qu’un pendule puisse facilement démontrer l’effet Foucault, il doit avoir un câble aussi long que possible et une masselotte symétrique lourde. Cependant, tous les pendules perdent un peu d’énergie à chaque oscillation en raison du frottement des courants d’air et des vibrations du câble et d’autres facteurs. Ainsi, laissé à lui-même, le pendule oscillerait en arcs de plus en plus courts jusqu’à ce qu’au bout de quelques heures, il diminue presque à zéro. Pour que le pendule de Foucault continue à fonctionner, il faut remplacer l’énergie perdue à chaque oscillation. Cela peut être fait en donnant au pendule un petit « coup de pied » à chaque oscillation.

Lorsque le pendule de Foucault était exposé au Musée National d’Histoire Américaine du Smithsonian aux Etats-Unis, pendant de nombreuses années (il a été retiré fin 1998), le maintient de l’oscillation du pendule de Foucault se faisait comme décris ci-dessous. Il existe bien sûr d’autres systèmes, mais grosso modo ils sont tous basés sur le même principe.

Pour ce faire, deux colliers en fer sont attachés au câble près du sommet. Un électroaimant en forme de beignet est intégré au plafond et le collier en fer oscille d’avant en arrière à l’intérieur du trou du beignet. Lorsque le câble du pendule atteint un point particulier de son oscillation, il est détecté par un dispositif électronique et l’aimant est activé au bon moment pour donner au collier (et donc au câble et au bob) un petit « coup de pied » dans la direction exacte de son oscillation naturelle. Cela restaure l’énergie perdue pendant l’oscillation et empêche le pendule de s’arrêter. Cela n’a aucun effet sur la direction de l’oscillation et n’interfère donc pas avec la démonstration de la rotation de la Terre.

Autre façon de procéder sur le même principe :

Si on s’en réfère au Bulletin de la SAF de novembre 1931, l’astuce de l’anneau de Charron est peu connue mais pourtant très efficace : on entretient le mouvement du pendule par un électroaimant très pointu et le cylindre est lui-même muni d’une pointe qui vient quasiment en contact de celle de l’électroaimant. Celui-ci est alimenté par un courant continu basse tension haché de la façon suivante : l’anneau de Charron (C) est placé à quelques décimètres du point d’oscillation O (pour une longueur de 1,70 m environ). Quand le fil de suspension métallique touche l’anneau très bien centré, le courant passe, il y a force électromagnétique attractive, donc retard vers la montée mais avance sur la descente. Puis aucune force lorsque le contact est perdu. Puis la symétrie pour l’autre côté. L’astuce consiste à ce que la bobine engendre un retard du courant : il y a donc bien gain global d’énergie. L’amplitude des oscillations (2 degrés environ) est imposée par le bilan énergétique. L’énergie perdue pendant une oscillation, qui croit avec l’amplitude, est exactement compensée par l’énergie fournie par l’électroaimant. Certes la période du pendule est composée de deux mouvements, l’un autour de O, et l’autre autour de (C) (de rayon très petit, 0,5 mm environ). On peut le vérifier par la mesure de T (en effectuant évidemment toutes les corrections qui s’imposent, en particulier fil d’acier maintenu en O par un mandrin cylindrique). L’originalité du système n’est pas qu’il entretienne le pendule, mais que le frottement solide du fil sur l’anneau (C) pendant une partie du mouvement, loin de perturber la précession, est au contraire un très subtil moyen pour supprimer l’influence des conditions initiales de lancement qui sont si critiques. Celui du Palais de la découverte fonctionnait sur ce principe. »

Enfin, depuis l’électronique a remplacé tout cela !