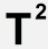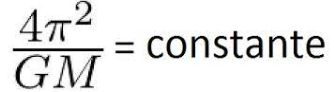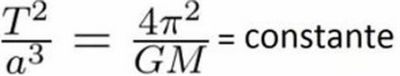La deuxième loi de Kepler

Elle est appelée aussi « Loi des aires ».

Cette loi démontre que le rayon vecteur qui relie le centre de la planète au foyer décrit des aires égales en des temps égaux. T’inquiète paupiette, tu vas comprendre. Regarde le schéma ci-dessous.

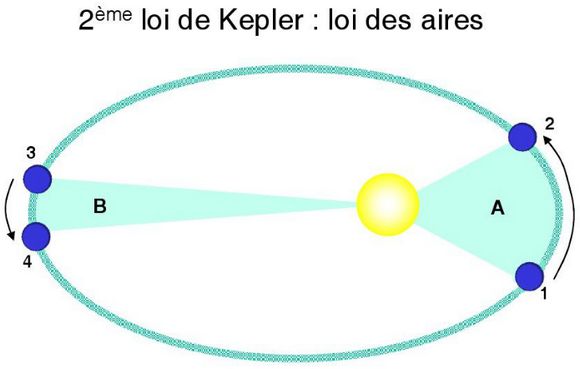
Tu reconnais l’ellipse. En jaune le soleil qui occupe un des foyers. Une planète suit donc son trajet elliptique. Elle passe obligatoirement lors d’une révolution (parcours complet de l’ellipse) par quatre points, 2 qui sont les plus proches du soleil (aphélie) et 2 qui sont le plus éloigné du soleil (périhélie).

Les 2 points les plus proches du soleil sont notées sur notre schéma 1 et 2, et les plus éloignées sont notées 3 et 4. Lors de sa révolution, la planète va mettre un certain temps pour franchir la distance de 1 à 2, et un autre temps pour franchir la distance de 3 à 4.

Kepler a observé, calculs mathématiques à l’appui évidemment, que le temps mis par la planète pour aller de 1 à 2 est le même que celui mis pour aller de 3 à 4. Pourtant la distance de 1 à 2 est bien plus importante que 3 à 4.

Également, les aires (surfaces) de la planète au Soleil sont de surfaces égales (même si leurs formes sont différentes), représentées sur le schéma par l’air A et l’aire B.

Quel est donc l’intérêt de cette deuxième loi dite Loi des aires ? Et bien il est extrêmement important, car il démontre de façon évidente que la vitesse d’une planète devient plus grande lorsque la planète se rapproche du Soleil. Cette vitesse est maximale au voisinage du rayon le plus court, le périhélie. Cette vitesse devient au contraire minimale au voisinage du rayon le plus grand, c’est-à-dire l’aphélie.

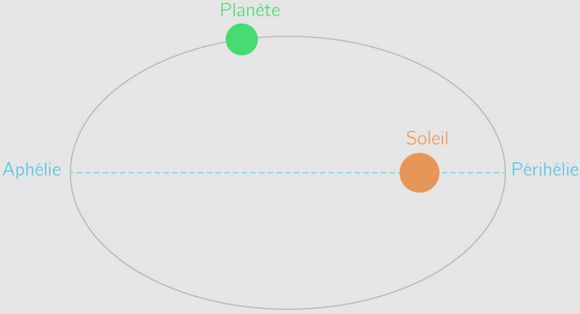
Les planètes en s’approchant du soleil accélère leur vitesse et en s’en éloignant ralentissent leur vitesse. La vitesse d’une planète sur son ellipse n’est donc pas constante.

Ainsi, le Soleil exerce une force puissante attractive des planètes vers lui. Nous savons que plus un objet tournant autour d’un point fixe est proche de ce point fixe, plus il tournera vite. A contrario, plus un objet est éloigné d’un point fixe en lui tournant autour, moins il ira vite. Le soleil a donc à une force d’attraction, de gravité, qui fait que la planète se rapprochant de lui accélère sa vitesse.

La troisième loi de Kepler

Elle est appelée « loi des périodes » ou « loi harmonique »

En 1619, Johannes Kepler publie le Harmonices Mundi (« L’Harmonie du monde » en cinq livres) dans lequel il fait un lien entre l’astronomie et la musique (ton serviteur est aux anges, puisque l’astronomie et la musique sont ses deux grandes passions !).

Dans cet ouvrage, il attribue aux planètes un thème musical. Les variations des vitesses de ces planètes sont représentées par les différentes notes composant la musique. Ainsi, il était facile de distinguer les orbites les plus excentriques. Ce qui est dit ici est exact, mais revenons à l’essentiel de cette troisième loi.

C’est dans cet ouvrage que Kepler énonce sa troisième loi fondamentale. Cette loi est une démonstration mathématique.

Le carré de la période de révolution est proportionnel au cube du demi-grand axe [de l'ellipse]. Celle-ci découle de ses recherches sur un modèle d’Univers harmonique. Cette loi permet de connaître la distance d'un corps au Soleil si on connaît sa période de révolution (=temps qu'il faut à la planète pour boucler son orbite). Celle-ci est relativement facile à mesurer alors que la distance l'est moins. Il y a donc un rapport constant entre la période de révolution et le rayon de l'orbite de la planète, donc sa distance par rapport au Soleil. On va essayer de la faire au plus simple.

Appelons le temps que met une planète pour faire sa révolution (le trajet complet de l’ellipse) T. Nous avons vu ci-dessus ce qui était le grand axe d’une ellipse. Pour rappel :

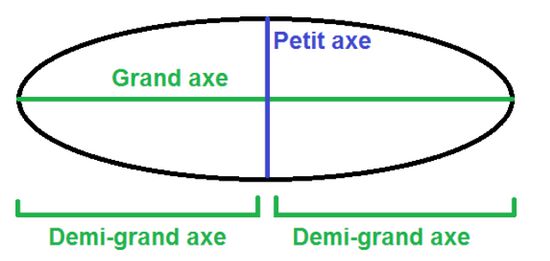
Le demi grand axe est représenté par le trait rouge de la figure ci-dessous :

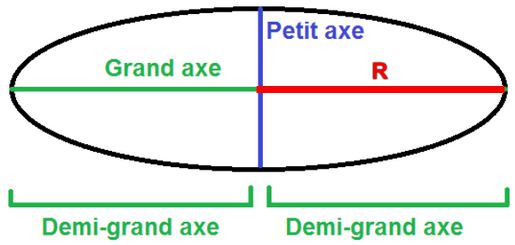
Nous nommerons ce demi grand axe R.

Le carré de la période de révolution est donc :

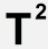
Le cube du demi-grand axe [de l'ellipse] est :

Et boum, on a la troisième loi de Kepler !

À partir du demi grand axe on peut déterminer la durée de révolution d’une planète, et réciproquement.

Oui, ami très curieux, tu vas me dire quelle est la constante ? Et bien pour cela il faut savoir que Newton a mis son grain de sel dans la formule de Kepler et l’a complétée. Cette constante souvent appelée K fait appel au carré du chiffre pi, à la constante de gravitation universelle G et enfin à la masse de l’astre centrales M autour duquel tourne les planètes ou satellites.

On a ainsi une constante comme suite :

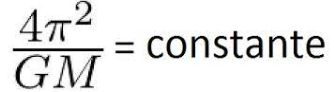
Ce qui nous donne la formule finale :

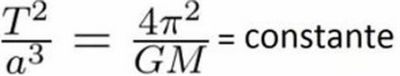
Dans cette formule le a = R du dessus

Et voilà, le tour est joué. À partir de là on peut connaître beaucoup de notions sur les planètes, dont la distance d'un corps au Soleil si on connaît sa période de révolution, et plein d’autres choses.

Voilà, ami désireux d’en savoir toujours plus, les trois lois de Kepler qui régissent le mouvement des planètes encore aujourd’hui.

Revenir à la page précédente