Johannes Kepler est né le 27 décembre 1571 et meurt le 15 novembre 1630. Il s’est inspiré des travaux de Nicolas Copernic, astronome allemand-polonais, célèbre pour avoir émis l’hypothèse héliocentrique, c’est-à-dire que la Terre et les autres planètes tournent autour du Soleil et non les planètes autour de la Terre.

Kepler affirme ainsi que la Terre tourne autour du Soleil, certes, mais surtout que les planètes ne tournent pas autour du Soleil en suivant des trajectoires circulaires parfaites mais des trajectoires elliptiques.

Kepler était persuadé que l’univers était créé par Dieu, mais que celui-ci a ordonné l’univers de façon extrêmement mathématique afin que l’homme puisse en comprendre le fonctionnement. Et il ne s’était pas trompé ! Pour Dieu, certains trouveront probablement à redire 12, pour le fonctionnement mathématique de l’univers Kepler l’a démontré. C’est lui qui a instauré les toutes premières lois de la physique mathématique qui relie les grandeurs de natures différentes dans l’univers. À son époque, il fallait le faire ! Et ça n’a pas été facile.

Les lois de Kepler ont été découvertes à partir des observations de Tycho Brahé (1546 - 1601) et de leurs analyses poussées par Johannes Kepler. Elles ont été démontrées par Isaac Newton (1642 - 1727) en 1687 dans les Principia, œuvre considérée comme un monument de la pensée humaine. On va voir tout ça, t’inquiète paupiette.

Pour énoncer ses lois, Kepler a travaillé de longues années, jours et nuits le plus souvent, allant d’essais infructueux en calculs erronés. À l’époque, les seules données astronomiques de référence étaient celle de Copernic. Mais le modèle de Kepler ne s’accordait pas avec les données de Copernic. Un des deux modèles se trompait. À ton avis, quel modèle Kepler privilégia-t-il ? Le sien of course !

Il fallait donc qu’il trouve des données plus exactes que l’hypothèse de Copernic. Il se tourne alors vers le danois Tycho Brahé (1546 – 1601) lequel ne parlait pas d’héliocentrisme comme Copernic, mais de géo-héliocentrisme. Le bonhomme était arrogant, dédaigneux, s’était attiré beaucoup d'inimitiés mais c’était un des astronomes les plus importants de tous les temps qui a eu le courage de laisser tomber toutes les traditions pour donner la priorité à l’observation par l’invention de ses instruments les plus précis au monde à l’époque. Il a fait ainsi sauter beaucoup de croyances astronomiques de l’époque qui ne reposait sur pratiquement rien.

Kepler avait une admiration sans bornes devant la rigueur et les connaissances scientifiques de Tycho Brahé. En arrivant à l’observatoire de Tycho Brahé, ce dernier a confié à Kepler l’étude de la planète Mars. Dans l’euphorie, Kepler a proposé à Tycho Brahé son étude et sa solution sur l’orbite de cette planète. Brahé dans son génie et sa rigueur scientifique transforma les huit jours d’études de Kepler sur Mars en 8 ans. Et c’est dans cette étude que Kepler découvrit que l’orbite de Mars n’était pas un cercle mais une ovale. Pour déterminer cette ovale il dut reprendre des centaines de fois ses calculs pour qu’ils correspondent aux observations. Et il est arrivé à la conclusion formelle que Mars avait une orbite elliptique.

L’homme peut saisir les lois puisque celles-ci sont fondées sur les nombres et sur la géométrie. C’est par cette conviction qu’il crée son premier modèle de mécanique céleste.

Kepler a découvert les relations mathématiques (dites Lois de Kepler) qui régissent les mouvements des planètes sur leurs orbites. Ces relations furent ensuite exploitées par Isaac Newton pour élaborer la théorie de la gravitation universelle.

Au même titre que Galilée ou Newton, le scientifique allemand Johannes Kepler compte parmi les fondateurs de la science moderne.

Ce qui est extraordinaire, ami patriote, c’est que ces lois datant du XVIIe siècle relative aux mouvements des planètes autour du Soleil, non contentes d'être encore pleinement d'actualité aujourd'hui, font autorité et servent de socle sur beaucoup d’autres études et découverte de l’univers encore de nos jours.

Kepler a donc étudié les mouvements des planètes (que l’on appelle la cinématique), complété par les lois de Newton pour en expliquer les causes (que l’on appelle la dynamique).

LES TROIS LOIS DE KEPLER

Et oui, elles sont au nombre de 3.

• Première loi : les planètes décrivent une ellipse dont le Soleil occupe l'un des foyers. Cette première loi décrit donc la forme des trajectoires.

• Deuxième loi : elle détermine les variations de vitesse le long de la trajectoire. Le rayon Soleil-planète balaie des aires égales pendant des intervalles de temps égaux

• Troisième loi : elle relie quantitativement deux grandeurs différentes liées à la trajectoire d’une planète, à savoir le temps qu’elle met à faire un tour et sa distance maximale soleil. Un peu plus mathématiquement, on peut dire de cette troisième loi que le carré de la période de révolution est proportionnel au cube du demi grand-axe de l'orbite.

Bon, voyons tout cela un peu plus en détail, mais t’inquiète paupiette, on va la faire simple…

La première loi de Kepler

Elle est appelée aussi « loi des orbites » ou « loi des ellipses ». Elle décrit la forme des orbites.

Il faut tout d’abord avoir une petite notion de ce qu’est une ellipse : c’est une courbe plane, fermée, dont tous les points sont tels que la somme de leurs distances à deux points fixes, appelée "foyer", est constante. On s’explique, ami.

Prend une forme brute de pomme comme celle de dessous :

Le trait arrondi qui définit cette forme est constitué d’une multitude de petits points que tu ne vois pas car ils sont collés les uns aux autres ne formant que la forme. On va donner la lettre M à tous ces petits points. Ainsi à la place du trait arrondi c’est comme s’il y avait des centaines de petits points, des centaines de fois la lettre M.

Avec cette forme, on a établi deux axes, un vertical et un horizontal :

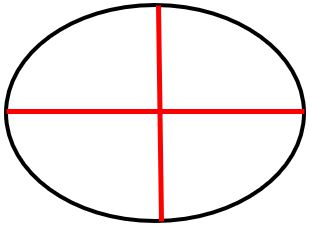
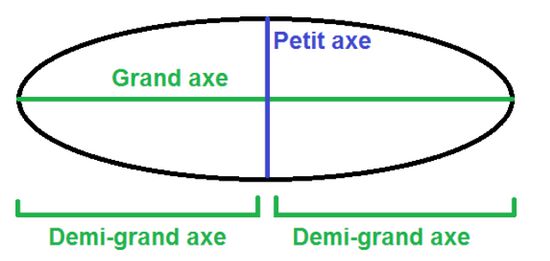
et pour plus de précision, voilà comment on les appelle quand on les considère entier ou à moitié.

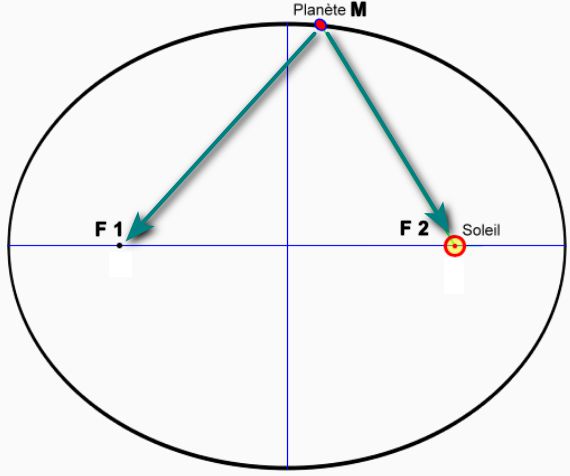
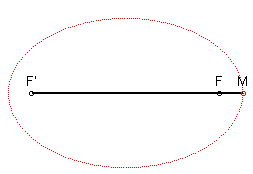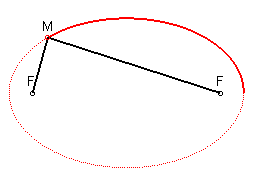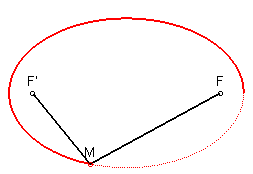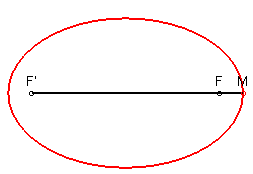
Plaçons sur le grand axe deux points, F1 et F2 appelés « foyers » ou « focus », et prenons un point sur la courbe à n’importe quel endroit appelé M (pointe du crayon) :

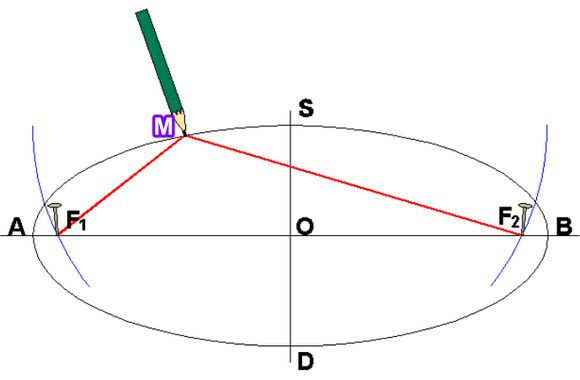
Pour que la forme soit qualifiée d’ellipse, il faut que la distance F1 à M et l’autre distance F2 à M présentent toutes les deux une somme toujours identique, constante. C’est-à-dire : F1-M + F2-M = constante. Tu vois, ce n’est pas bien compliqué.

Mais alors, si F1 et F2 sont confondus en un seul point que l’on appellera O, que se passe-t-il ? Tout simplement nous ne parlerons plus d’ellipse mais de cercle. Effectivement, chacune des deux distances F1-M et F2-M sont toujours égales et formes le rayon du cercle.

Tu l’as compris, ami passionné d’astronomie, les points F1 et F2 constituant les deux foyers de l’ellipse sont les foyers du soleil, et le point M constitue une planète. On a ainsi :

Et parce que c'est toi, une petite animation qui montre la même chose :

Suite >